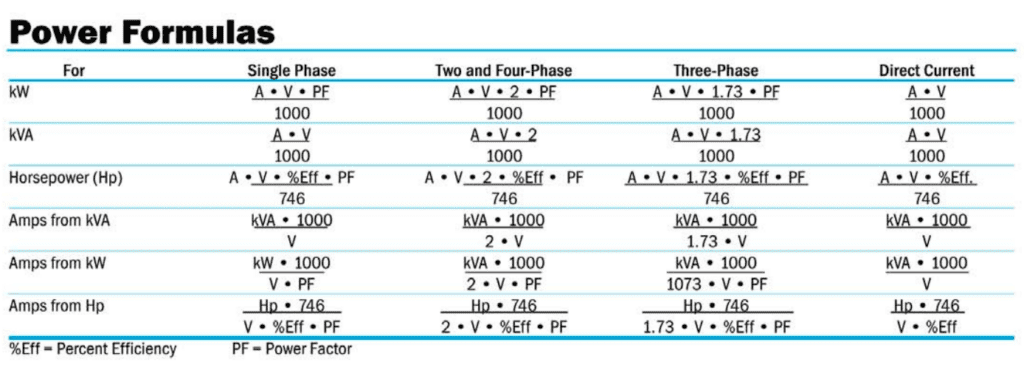
Power is the rate at which work is done (work/time). It is also the rate at which energy is generated or used. For dc systems, power is expressed in watts: P=VdcAdc. For ac systems, the determination of power is more complex. The voltage and current in an AC circuit periodically change direction (alternating current). In a purely resistive circuit, the voltage and current change direction at the same time (in-phase). Power measurements are made by measuring the RMS current and voltage and applying the formula P = VrmsArms.
If a reactive element is also present (either capacitive or inductive), the voltage and current no longer change direction at the same time. Current will lag the voltage when the circuit includes inductance (see fig. A). Current will lead the voltage when the circuit includes capacitance. The amount of lead or lag, expressed in degrees, is the phase angle (ø). The power delivered is P = VAcosø. The term cosø is the power factor. Note that for a purely reactive circuit, P = 0.
A load that includes reactive elements is a complex impedance (Z). In a series circuit Z = √÷R2, where X is the inductive or capacitive reactance in ohms and R is the resistance in ohms. In a parallel circuit Z = RX/√÷R2. Power factor is the ratio R/Z. Power factor can also be described as the true power divided by the apparent power: PF = W/VA. For a purely resistive circuit, PF = 1.
Crest Factor
Another parameter used to characterize ac voltage and current waveforms is the crest factor – the ratio of peak to RMS value. The crest factor of a sine wave is. CF of a full-wave rectified sine is also √2, but a half-wave rectified sine is 2. The CF of a square wave is 1; triangle wave √3. Low duty cycle pulse trains can have crest factors >10.
The crest factor specification in a measuring instrument defines the peak signal level that can be handled, often with a derated accuracy.
Two factors contribute to this specification:
– Dynamic range of the amplifiers and signal conditioning circuits
– Bandwidth of the RMS converter used.
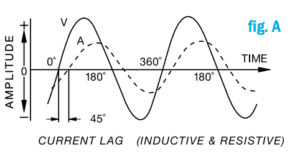
On instruments with more than one input range, a limitation in the amplifiers can be overcome by using a higher range. The signal peaks for a particular amplitude will then fall within the maximum allowed on that range (fig. B).
As crest factor increases, the higher frequency components become a larger part of the total waveform. These are usually multiples of the fundamental frequency (harmonics). Electronic speed controls, lamp dimmers, switching power supplies and similar electronic circuits often generate waveforms with high harmonic content. A single-phase diode bridge DC power supply, with no line filtering, has current waveform harmonics well beyond the 7th (see fig. C).
A converter with bandwidth (-3db point) of 780Hz will measure 71% of the contribution of the 13th harmonic. Converter bandwidth is not a major problem when the fundamental is 50 or 60Hz. However, when the fundamental is a high frequency (e.g. 20kHz in a power inverter) much greater bandwidth is required to accurately measure a non-sinusoidal waveform. Test equipment intended to measure points within a switching circuit need high bandwidth.
Single Phase Circuits
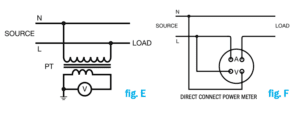The simplest single-phase ac power connection requires two wires. In low voltage circuits, voltage can be measured directly with an appropriately scaled ac voltmeter. Current is usually measured by inserting a current transformer in the line side and monitoring the output with a 5A full-scale ac ammeter (fig. D). Where the circuit cannot be broken to insert the current transformer, a split core or clamp-on current transducer can be used. In higher voltage circuits, a potential transformer may be added to step down the source voltage to a lower level (fig. E).
Depending on voltage levels, frequency meters can be directly connected in the same manner as the ac voltmeter or operated through a potential transformer. Some wattmeters, power factor meters and watt-hour meters are directly connected to the power source (fig. F). In higher energy circuits, or situations where the meter is located far from the power circuit, a CT and PT are used (fig. G).
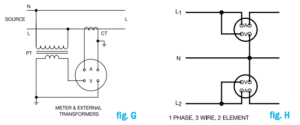In a single-phase three-wire system, the two hot conductors are 180° out of phase (referenced to the neutral). A single-phase three-wire system requires two single-phase wattmeters or one polyphase instrument with two measuring elements (each element measures voltage and current). This is shown in fig. H. Care must be taken not to overload the meter when power factor is low. With PF=0.5, a full-scale readout requires 2X full scale on either the V or A input.
Polyphase Circuits
While many of the loads throughout a plant are single-phase, their operating power comes from one phase of a three-phase distribution system. Heavy electrical loads, such as large motors, are generally three-phase for improved efficiency. Three-phase power is configured as either wye (Y) or delta. Y connections can be either 3 or 4 wire. The voltage on each phase is displaced by 120° from the voltage on the other phases.
Blondel’s Theorem states that if a network is supplied through N conductors, the total power is measured by summing the readings of N wattmeters arranged so a current element of a wattmeter is in each line and the corresponding voltage element is connected between that line and a common point. If the common point is located on one of the lines, then the power may be measured by N-1 wattmeters.
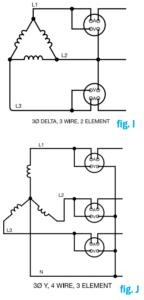
This allows a 3 phase, 3-wire system to be measured by two single-phase wattmeters, similar to the single-phase, three-wire system (see fig. I).
Total power is the algebraic sum of the two readings under all conditions of load and power factor. If the load is balanced, at unity power factor, each instrument will read half the load; at 0.5 power factor one instrument reads all the load and the other reading is zero; at less than 0.5 power factor one reading will be negative. While balanced loads are preferred, many systems today are unbalanced due to system modifications or the presence of non-linear loads.
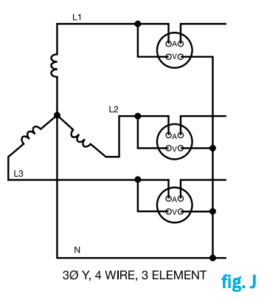
A 3 phase Y system with a center neutral is the equivalent of a 4-wire system. It requires the use of three measuring elements (fig. J). With three wattmeters, total power is the algebraic sum of the three readings under all conditions of load and power factor.
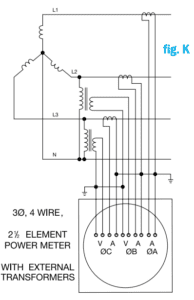These diagrams show the use of single-phase, directly connected wattmeters. External PTs and CTs can also be used as discussed for single-phase circuits. In practice, a three-phase power meter is normally used, since it can measure all three legs and perform the algebraic sum internally. In systems where the third voltage lead is not available at the meter, a special 2 1 /2 element configuration can be used, as shown in fig. K.
Polyphase instruments are available in both analog and digital configurations. Some electronic 3 phase power meters cannot be used on single-phase circuits, due to the internal math function required.
Energy
Energy is power used for a certain time (P ˚ t). Electrical energy is normally measured in kWh or MWh. Kilowatt-hour meters are power meters with a timebase for integrating the instantaneous power over time. Electronic versions of the kWH meter often include the ability to display power and demand. Demand is the average amount of energy consumed over a specific time interval. For a utility, this interval is usually 15 or 30 minutes. The utility must have sufficient capacity to supply the peak demand, so energy prices are often established based on this factor. Demand meters with adjustable setpoints and output relays can be used to shed low priority loads to limit demand peaks. Demand readout on an analog kWh meter is implemented with a manually reset drag pointer.
